Evolution equations

(See the introduction here

The evolution of a dynamical system depending on a continuous time variable $t$ is described by an equation of the form:

$$\dot{u}=f(u).$$

Here, the dot denotes a time derivative, $u(t) \in X$ is the state of the system at time $t$, and $f$ is a given vector field on $X$. The space $X$ is the state space of the system; a point in $X$ specifies the instantaneous state of the system. We will assume that $X$ is a Banach space. When $X$ is finite dimensional, the evolution equation is a system of ODEs.

Infinite dimensional case

On the other hand, some PDEs can be regarded as evolution equations on an infinite dimensional state space $X$ (see example in Classical Field Theory). The solution $u(x,t)$ is an element of an specific function space $\mathcal F$ at each instant of time $t$, yielding a curve in $\mathcal F$. In the finite dimensional case you can consider that the finite number of entries $u^1(t), u^2(t), \cdots,u^{n}(t)$ is like a function of two variables, a continuous variable $t\in \mathbb{R}$ and a discrete one $i=1,\ldots,n$. Now, think that the index $i$ in $u^i$ is substituted by $x$ in $u(x)$: we have an uncountable set of entries, and the derivatives of each of them needs to be related to the entries themselves. The problem in general would be intractable: how would we write infinite relations between $u(1,t),u(2,t),u(3,t),u(8.23,t),\ldots$?

But we can restrict to special cases of "relations" between the "components" $u(x)$, or better said, special patterns: the derivatives of $u$ respect to $x$. For example, $u_t=u_x$ would play the role of an infinite collection of expressions analogous to $\frac{d}{dt}u^i=u^{i+1}-u^i$... See xournal_210.

So an evolution equation, in this context, is an expression

where $x\in \mathbb{R}$, $u\in \mathbb{R}$ and $u^{(n)}=(u,u_x,u_{xx},\ldots)$. This can be further generalized (@olver86 page 303).

The differential function $Q$ can be seen as a kind of vector field on the space of functions $\mathcal F$, whose flow is denoted by $\mbox{exp}(t V_Q):t\to u(-,t)\in \mathcal{C}^{\infty}$. It is associated to the evolutionary vector field $V_Q$ in the following sense: given a differential function $P([u])$ then

measures the variation of $P$ at $f(-)\in\mathcal{C}^{\infty}(U)$ in the direction of the flow $t\mapsto u(-,t) \in\mathcal{C}^{\infty}(U)$ created by $Q$. We could even write a kind of Lie series

In particular if $P$ is the identity, we have a formal solution to the evolution equation.

On the other hand, suppose that the evolutionary vector field $V_Q$ is a symmetry of an ODE $\Delta=0$, that is,

The differential function $\Delta$ can be though as a kind of first integral for the evolution equation. Indeed, if $\Delta$ is of order, let's say, 2, then we can think of it like $\infty-2$ first integrals...

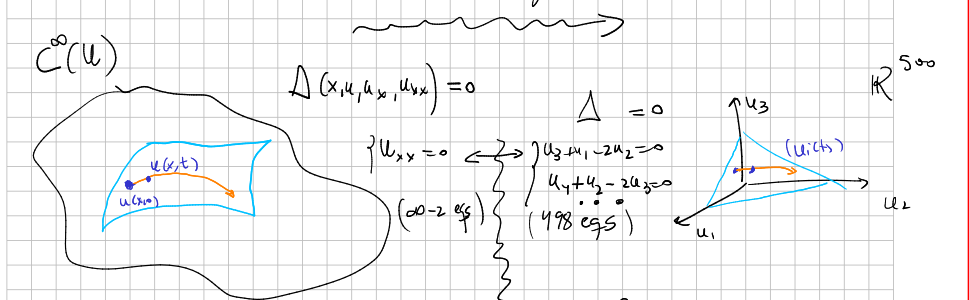
xournal_210

And I wonder, can any evolution equation be characterized by 2 second-order ODEs? It would be like an implicit expression of the PDE...

And another question: in the context above, is $\Delta$ a conservation law of

??

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es